WGCNA: Weighted gene co-expression network analysis
This code has been adapted from the tutorials available at WGCNA website. For the installation and more detailed analysis, please visit the website.
Getting started: in order to run R on Orchestra, we will first connect to an interactive queue
# bsub -n 2 -Is -q interactive bash
# git clone https://github.com/hms-dbmi/scw.git
# cd scw/scw2016
# source setup.sh
# R
Loading WGCNA library, and settings to allow parallel execution. Please note that WGCNA and dependencies have been already installed for you.
library(WGCNA)
library("flashClust")
options(stringsAsFactors = FALSE);
#enableWGCNAThreads()
disableWGCNAThreads()
Loading the data; WGCNA requires genes be given in the columns. For the purpose of this exercise, we focus on a smaller set of n=500 most variable/over-dispersed genes:
load('data/varinfo.RData');
mydata=varinfo$mat;
dim(mydata)
## [1] 12453 224
gene.names=names(sort(varinfo$arv,decreasing=T));
mydata.trans=t(mydata);
n=500;
datExpr=mydata.trans[,gene.names[1:n]];
SubGeneNames=gene.names[1:n];
Choosing a soft-threshold power: a tradeoff between scale free topology and mean connectivity
powers = c(c(1:10), seq(from = 12, to=20, by=2));
sft=pickSoftThreshold(datExpr,dataIsExpr = TRUE,powerVector = powers,corFnc = cor,corOptions = list(use = 'p'),networkType = "signed")
## Power SFT.R.sq slope truncated.R.sq mean.k. median.k. max.k.
## 1 1 0.147 27.10 0.939 252.0000 2.51e+02 259.00
## 2 2 0.229 -11.10 0.620 129.0000 1.28e+02 141.00
## 3 3 0.590 -9.73 0.598 66.5000 6.55e+01 81.80
## 4 4 0.786 -7.17 0.728 35.0000 3.38e+01 50.20
## 5 5 0.899 -5.48 0.881 18.7000 1.76e+01 32.60
## 6 6 0.915 -4.17 0.922 10.2000 9.19e+00 22.40
## 7 7 0.899 -3.26 0.930 5.6600 4.83e+00 16.00
## 8 8 0.901 -2.66 0.910 3.2300 2.56e+00 12.00
## 9 9 0.903 -2.22 0.932 1.9000 1.36e+00 9.22
## 10 10 0.896 -1.93 0.924 1.1600 7.25e-01 7.27
## 11 12 0.954 -1.60 0.966 0.4820 2.10e-01 4.91
## 12 14 0.968 -1.41 0.964 0.2330 6.26e-02 3.52
## 13 16 0.960 -1.28 0.949 0.1290 1.91e-02 2.60
## 14 18 0.961 -1.21 0.953 0.0778 5.98e-03 1.95
## 15 20 0.947 -1.15 0.933 0.0501 1.88e-03 1.48
# Plot the results
# sizeGrWindow(9, 5)
par(mfrow = c(1,2));
cex1 = 0.9;
# Scale-free topology fit index as a function of the soft-thresholding power
plot(sft$fitIndices[,1], -sign(sft$fitIndices[,3])*sft$fitIndices[,2],xlab="Soft Threshold (power)",ylab="Scale Free Topology Model Fit, signed R^2",type="n", main = paste("Scale independence"));
text(sft$fitIndices[,1], -sign(sft$fitIndices[,3])*sft$fitIndices[,2],labels=powers,cex=cex1,col="red");
# Red line corresponds to using an R^2 cut-off
abline(h=0.80,col="red")
# Mean connectivity as a function of the soft-thresholding power
plot(sft$fitIndices[,1], sft$fitIndices[,5],xlab="Soft Threshold (power)",ylab="Mean Connectivity", type="n",main = paste("Mean connectivity"))
text(sft$fitIndices[,1], sft$fitIndices[,5], labels=powers, cex=cex1,col="red")

Generating adjacency and TOM similarity matrices based on the selected softpower
softPower = 5;
#Calclute the adjacency matrix
adj= adjacency(datExpr,type = "signed", power = softPower);
#Turn adjacency matrix into a topological overlap matrix (TOM) to minimize the effects of noise and spurious associations
TOM=TOMsimilarityFromExpr(datExpr,networkType = "signed", TOMType = "signed", power = softPower);
## TOM calculation: adjacency..
## adjacency: replaceMissing: 0
## ..will not use multithreading.
## Fraction of slow calculations: 0.000000
## ..connectivity..
## ..matrix multiplication..
## ..normalization..
## ..done.
colnames(TOM) =rownames(TOM) =SubGeneNames
dissTOM=1-TOM
Module detection
#Hierarchical clustering of the genes based on the TOM dissimilarity measure
geneTree = flashClust(as.dist(dissTOM),method="average");
#Plot the resulting clustering tree (dendrogram)
plot(geneTree, xlab="", sub="",cex=0.3);

# Set the minimum module size
minModuleSize = 20;
# Module identification using dynamic tree cut, you can also choose the hybrid method
dynamicMods = cutreeDynamic(dendro = geneTree, method="tree", minClusterSize = minModuleSize);
#dynamicMods = cutreeDynamic(dendro = geneTree, distM = dissTOM, method="hybrid", deepSplit = 2, pamRespectsDendro = FALSE, minClusterSize = minModuleSize);
#Get the module labels and the size of each module. Lable 0 is reserved for unassigned genes
table(dynamicMods)
## dynamicMods
## 0 1 2
## 253 159 88
#Plot the module assignment under the dendrogram; note: The grey color is reserved for unassigned genes
dynamicColors = labels2colors(dynamicMods)
table(dynamicColors)
## dynamicColors
## blue grey turquoise
## 88 253 159
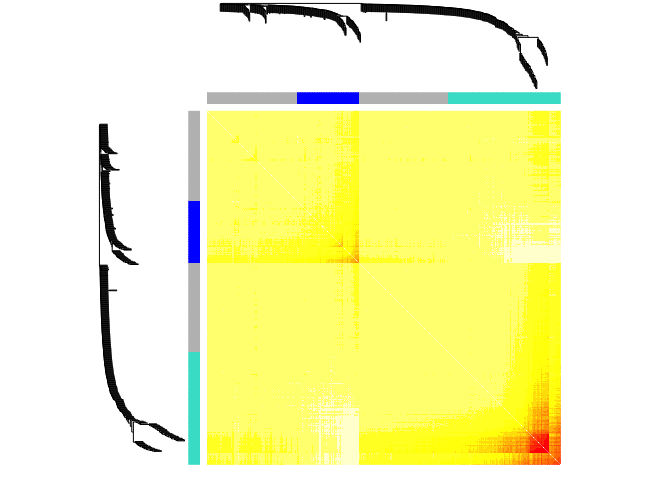
plotDendroAndColors(geneTree, dynamicColors, "Dynamic Tree Cut", dendroLabels = FALSE, hang = 0.03, addGuide = TRUE, guideHang = 0.05, main = "Gene dendrogram and module colors")

#Set the diagonal of the dissimilarity to NA
diag(dissTOM) = NA;
#Visualize the Tom plot. Raise the dissimilarity matrix to a power to bring out the module structure
#sizeGrWindow(7,7)
TOMplot(dissTOM^4, geneTree, as.character(dynamicColors))
Extract modules
module_colors= setdiff(unique(dynamicColors), "grey")
for (color in module_colors){
module=SubGeneNames[which(dynamicColors==color)]
write.table(module, paste("module_",color, ".txt",sep=""), sep="\t", row.names=FALSE, col.names=FALSE,quote=FALSE)
}
Look at expression patterns of these genes, as they are clustered
module.order <- unlist(tapply(1:ncol(datExpr),as.factor(dynamicColors),I))
m<-t(t(datExpr[,module.order])/apply(datExpr[,module.order],2,max))
heatmap(t(m),zlim=c(0,1),col=gray.colors(100),Rowv=NA,Colv=NA,labRow=NA,scale="none",RowSideColors=dynamicColors[module.order])

We can now look at the module gene listings and try to interpret their functions; for instance using http://amigo.geneontology.org/rte
WGCNA has many more features, such as quantifying module similarity by eigengene correlation, etc. For details, please visit WGCNA website.
